



Some Helpful Tools
Math: Decimals and Operations - Tutorial
This section will cover the fundamentals and rules for decimals.
Place Value
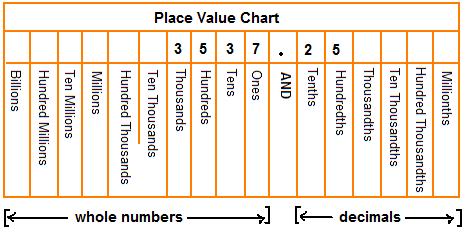
The number system contains an infinite amount of numbers. Each digit has its own place and value.
Example 1: How would you read 3,537.25?
Answer: three thousand five hundred thirty-seven and twenty-five hundredths.
Example 2: How would you read 23.734?
Answer: twenty-three and seven hundred thirty-four thousandths.
Keep in mind that only the last digit to the right of the decimal has the "ths" ending.
Example 3: How woud you read 107.15?
Answer: one hundred seven and fifteen hundredths.
Example 4: How woud read .39?
Answer: thirty-nine hundredths
Decimals and Zeros
Zeros are placeholders that show the value of a number.
Example 1: .2 is read as: two tenths
Example 2: .02 is read as: two hundredths
Example 3: .002 is read as: two thousandths
The more zeros you add, the further you are moving away from the whole number. So the numbers are getting smaller. It all depends on where you place the zero.
For example:
.5 and .50 have the same value.
However,
.05 is less than .5.
Decimal places represent fractional values. Fractions represent a part of a whole.
Let's compare two decimals.
Which number has the larger value? .25 and .147
To answer this question, line up the numbers by their decimals. Then add a zero to make the digits the same.
.25 = .250
.147 = .147
You can see that .147 is smaller than .250 because 147 is less than 250. Therefore,
.25 has a larger value than .147.
Rounding Decimals
Example 1:
Suppose you are solving a word problem involving money, and you have arrived at the answer $129.238. You are told to round your answer to the nearest cent.
Begin by remembering the place values to the right of the decimal point.
$129.238
.2 = two tenths
.23 = twenty-three hundredths
.238 = two hundred thirty-eight thousandths
Look at the number that is in the thousandths place.
Remember, when rounding anything 5 or more is rounded up. Anything less than five remains the same.
The answer is $129.24
Example 2: Round $219.762 to the nearest cent.
The answer is $219.76
Example 3: Round $129.24 to the nearest dollar.
To do this, look at the first number to the right of the decimal point. In this case, the number is 2. Since 2 is less than 5, the 9 remains the same.
The answer is $129.00
Example 4: Round $219.76 to the nearest dollar.
The answer is $220.00
Rounding Decimals
When adding or subtracting decimals, remember to line up the decimal points.





Example:
When multiplying decimals, remember to count the decimal places.
Example:
Since there are three decimal places, move the decimal point over three places to the right.
The answer is 2.457
When dividing decimals, count the number of decimal places in the divisor. Then move that many places over in the dividend and place the decimal directly above
the decimal point in the dividend as shown below.
Example:
rewrite as:
Note:
Place a bar above the first six after the decimal to show that it repeats.
Putting Decimals in Order
A string of decimals can be arranged in order according to size.
Example 1: Put the following decimals in order from the smallest to the largest.
3.74 3.37 3.8 3.059
Remember to line up the decimal points and add zeros to make the digits the same.
Since the whole numbers are the same, look at the digits in the tenths place to help arrange the decimals in the correct order.
Example 2: Put the following decimals in order from the largest to the smallest.
5.047 5.028 5.13 5.097
5.074
5.028
5.130
5.097
Hint:
Look at the numbers that are in the hundredths place
as well as the tenths place.
5.13 5.097 5.074 5.028
(from the largest to the smallest)